Reanalysis Comparison Update 2023

This post provides a brief comparison update of two different reanalysis daily global mean surface air temperature anomaly (GMSATA) time series for 2014 through 2023 January 31. The graph in Figure 1 shows the daily GMSATA time series for the Climate Forecast System Reanalysis (CFSR) output based on the Global Forecast System (GFS) initialization output four times each day. The temperature output is for the atmosphere at 10 meters above ground level. The CFSR model uses a 0.5 degree latitude by 0.5 degree longitude grid.

Figure 1. CFSR GMSATA 2014-2024 (click on image to enlarge)

The graph in Figure 2 shows the daily GMSATA time series for the Sigma 0.995 level output from the National Centers for Environmental Prediction and National Center for Atmospheric Research Reanalysis 1 (NCAR R1) cooperative effort. The Sigma 0.995 level corresponds to the pressure altitude at 99.5 % of the surface air pressure, which is roughly about 50 meters above ground level. The actual height above ground level varies somewhat depending on atmospheric conditions. The NCAR R1 model uses a 2.5 degree latitude by 2.5 degree longitude grid.

Figure 2. NCAR R1 GMSATA 2014-2024 (click on image to enlarge)

Figure 3 provides the NCAR R1 daily GMSATA time series for the current century beginning in 2001.

Figure 3. NCAR R1 GMSATA 2001-2024 (click on image to enlarge)

For a broader perspective, Figure 4 provides the NCAR R1 daily GMSATA time series for its entire period of record, beginning in 1948.

Figure 4. NCAR R1 GMSATA 1948-2024 (click on image to enlarge)

Reanalysis Comparison Update 2022

This post provides a quick comparison update of two different reanalysis daily global mean surface air temperature anomaly (GMSATA) time series for 2014 through 2022 March 19. The graph in Figure 1 shows the daily GMSATA time series for the Climate Forecast System Reanalysis (CFSR) output based on the Global Forecast System (GFS) initialization output four times each day. The temperature output is for the atmosphere at 10 meters above ground level. The CFSR model uses a 0.5 degree latitude by 0.5 degree longitude grid.

Figure 1. CFSR GMSATA 2014-2023

The graph in Figure 2 shows the daily GMSATA time series for the Sigma 0.995 level output from the National Centers for Environmental Prediction and National Center for Atmospheric Research Reanalysis 1 (NCAR R1) cooperative effort. The Sigma 0.995 level corresponds to the pressure altitude at 99.5 % of the surface air pressure, which is roughly about 50 meters above ground level. The actual height above ground level varies somewhat depending on atmospheric conditions. The NCAR R1 model uses a 2.5 degree latitude by 2.5 degree longitude grid.

Figure 2. NCAR R1 GMSATA 2014-2023

Figure 3 provides the NCAR R1 daily GMSATA time series for the current century beginning in 2001.

Figure 3. NCAR R1 GMSATA 2001-2023

For a broader perspective, Figure 4 provides the NCAR R1 daily GMSATA time series for its entire period of record, beginning in 1948.

Figure 4. NCAR R1 GMSATA 1948-2023

Hunga-Tonga Eruption 2022

Preliminary estimates indicate that the massive Hunga-Tonga explosive eruption 2022 January 15 was the most intense since the Pinatubo explosive eruption in 1991. The eruption sent ash and sulfur dioxide well into the stratosphere, but preliminary estimates of the amount appears to be at least a factor of 4 to 5 lower than from Pinatubo. Consequently, the effect on global weather may not be very significant. However, the eruption was quite impressive nonetheless. Below is an animation of daily Suomi NPP satellite images with the stratospheric sulfur dioxide analysis superimposed in blue.

Figure 1. NASA Worldview depiction of Suomi NPP daily satellite composite images with superimposed stratospheric sulfur dioxide in blue for 2022 January 13 through 21 (click on image to enlarge).

A wide view of the first several hours of the eruption as seen in GeoColor images from NOAA GOES-17 from 0100 to 1250 UTC on 2022 January 15 is included in the animation below.

Figure 2. NOAA GOES-17 GeoColor animation for the Southwest Pacific on 2022 January 15 (click on image to enlarge).

A cropped closer view of the 0400 to 0600 UTC portion of the eruption is provided below at 10-minute intervals.

Figure 3. NOAA GOES-17 GeoColor animation at 10-minute intervals from 0400 through 0600 UTC on 2022 January 15 (click on image to enlarge).

From Wikipedia: “The eruption column rose 55 kilometres (34 mi) into the mesosphere and contained approximately 2–2.6 km3 (0.48–0.62 cu mi) of material, roughly twice that of the 1980 eruption of Mount St. Helens.” And quite a bit less than the estimated 10 km3 (2.4 cu mi) of material from Pinatubo in 1991, but the most since that time.

A potentially big difference between the Hunga-Tonga and Pinatubo eruptions is that the Hunga-Tonga eruption probably blasted huge amounts of ocean water into the statosphere and possibly all the way into the mesosphere. That could include salt particles as well as ice crystals, in addition to the sulfates forming from sulfur dioxide emitted.

Sea Level Rise Catastrophe ?

Lately there have been numerous claims of a coming sea level rise catastrophe resulting from the “climate crisis” supposedly driven by ever increasing fossil fuel related emissions of carbon dioxide.  The claims include coastal sea levels rising a meter or more over coming decades and inundating many coastal cities.  I decided to examine the actual coastal sea level measurements to see what they show regarding these extraordinary claims.  What I found is that coastal sea level measurements indicate that the long-term absolute coastal sea level rise is not accelerating and is not alarming.  In fact, it is consistent with what humans have dealt with over the last 150 years and nothing worse.

Sea level changes are very important to human activities and interests at coastal locations, especially in populated areas.  However, what happens in the middle of oceans is of little consequence in this regard.  Thus, I have focused on coastal measurements.  Sea level monitoring at some coastal locations began over 100 years ago.  From these longer periods of record, coastal sea level trends can be evaluated over time and compared among locations.

First, there are several important factors to consider for coastal sea level measurements.  Most importantly, the land can rise or fall over time relative to the center of the earth and this change can significantly affect the relative sea level change measured at a given location over time.  A lesser, but sometimes important effect can occur from change in elevation of the measurement station relative to the overall nearby land surface, such as from a heavy concrete dock slowly sinking into the surrounding mud over time for instance.  Also, measurement methods vary from station to station and over time which can introduce artificial differences.  Another factor is that sea level at some locations is much more variable over time because of tides and/or storm surge and associated variations over time.  Furthermore, sea level at some locations is influenced by changing regional sea surface temperature patterns, such as tropical locations where sea level is affected by El Niño and La Niña related patterns.

The plots provided in this post come from the Sealevel website and have seasonal fluctuations removed.  I looked for measurement locations with continuous or nearly continuous 100-year or longer periods of record extending to the present.  Then I checked for locations with recently stable vertical land motion.  Locations with stable vertical land motion are most likely to better represent absolute coastal sea level change. Stations where the land is rising or falling are measuring relative sea level change and the vertical land motion must be considered to estimate the absolute sea level change.  I found 15 long-term sea level  measurement sites with nearby or collocated Continuous Global Positioning System (CGPS) measurements.  Sea level measurements from seven of these sites are presented  below.

To estimate the vertical land motion, I looked at nearby CGPS estimates of land motion trends using the Sonel website.  For some locations there were no nearby CGPS measurements available, so I disregarded those sites for this analysis.  For the remaining sites, most had CGPS measurements from nearby locations that were not collocated with the sea level monitoring site, which increases uncertainty a bit.  Fortunately, the site with the smallest vertical land motion has the CGPS monitor collocated with the sea level monitoring site at Honolulu, Hawaii.  Measurements from this site, as displayed in Figure 1 below, indicate a sea level trend of about 1.49 +/- 0.21 millimeters per year (mm/yr) for 1905-2017.  The recent CGPS land vertical motion trend for 1999-2014 was -0.23 +/- 0.18 mm/yr or practically stable considering the uncertainty.  These measurements indicate a global coastal absolute sea level rise of about 15 centimeters (6 inches) over 100 years with no acceleration – certainly not alarming and no different than what has already been handled over the last 100 years.

Figure 1. Honolulu HI USA 1612340 (click to enlarge)

The graph in Figure 1 also includes a plot of ice core and Mauna Loa carbon dioxide (CO2) levels in conjunction with the sea level measurements.  As can be seen, there is no indication of acceleration in the sea level rise associated with the accelerating rise of atmospheric CO2.  The implication is that we are not likely to see an effect on sea level rise from increasing CO2 levels any time soon, or we already would be seeing the effect.

The site with the second most stable land motion was at Trieste, Italy where the indicated sea level rise for 1875-2016 was 1.30 +/- 0.15 mm/yr as seen in Figure 2 below, with a recent land vertical motion trend of 0.32 +/- 0.26 mm/yr.  Here the CGPS site was not collocated with the sea level monitoring site and thus there may be a larger uncertainty about the land motion at the sea level monitoring site.  This uncertainty is probably enough to account for the difference in the sea level rise from that measured at Honolulu.  However, once again there is no indication of any significant sea level rise acceleration over the last 100 years at Trieste, despite the accelerating rise in CO2 levels.

Figure 2. Trieste Italy 270-061 (click to enlarge)

Of the remaining sites, nine had nearby or collocated CGPS measurements indicating land motion trends of -0.53 to -4.59 mm/yr (subsiding land) and four sites had land motion indicated in the range from 0.59 to 7.88 mm/yr (rising land).  Figures 3, 4, and 5 show sea level trends for locations with subsiding land: San Francisco, California; New York City (The Battery), New York; and Galveston, Texas.  Nearby CGPS measurements indicated vertical land motion trends of -0.84 +/- 0.18 mm/yr at San Francisco, -2.12 +/- 0.62 mm/yr at New York City, and -4.59 +/- 0.78 mm/yr at Galveston (all with subsiding land).  The measured relative sea level rise rates are listed in the graphs.

Figure 3. San Francisco CA USA 9414290 (click to enlarge)

Figure 4. The Battery NY USA 8518750 (click to enlarge)

Figure 5. Galveston TX USA 8771450 (click to enlarge)

The relative sea level measurements at two locations with CGPS indicated rising land motion are displayed in Figures 6 and 7 for Oslo, Norway and Vaasa, Finland.  Nearby CGPS measurements indicated recent rising land motion of 5.33 +/- 1.12 mm/yr at Oslo and 7.88 +/- 1.14 mm/yr at Vaasa.

Figure 6. Oslo Norway 040-321 (click to enlarge)

Figure 7. Vaasa Finland 060-051 (click to enlarge)

Yet again, there is no indication of accelerating sea level rise at San Francisco, New York City, or Galveston or corresponding decelerating sea level fall at Oslo and Vaasa as might be expected if accelerating atmospheric CO2 levels were having an impact.  Sea level rise will be enhanced at locations where land is subsiding.  Galveston is a good example, where the land is subsiding faster than the sea is rising – a bad combination.  And there are many other coastal locations in the same predicament, but it’s the land subsidence that is the main problem at these locations.

Extraordinary claims require extraordinary evidence, and the evidence clearly does not support the claims.  The claims of dire sea level rise in coming decades are pure speculation at best and fearmongering at worst.

Climate and Weather Extremes

We evaluate climate using statistical summaries of weather data collected over longer time periods, including means, percentiles, and extremes of various weather parameters such as temperature, precipitation, and wind.  Climate can be evaluated on spatial scales ranging from global to regional to local and even micro-scale and for temporal scales ranging from days to months to seasons to years to decades to centuries to millennia and beyond.  Weather extremes are part of climate and both weather and climate vary depending on temporal and spatial scales.  In general, the magnitude of variation of both climate and weather extremes is likely to be larger over longer time scales.  This complexity makes evaluating climate trends and associated extreme weather event trends very difficult.  Any evaluation is relative – both spatially and temporally.

However, some simple statistics can be applied to examining weather extremes.  If we choose a local spatial scale and a millennia time scale, we can look at probabilities of the occurrence of extreme weather events, such as extreme cold and hot temperatures, extreme precipitation, and extreme drought for instance.  If we assume extreme weather events are random and select 1,000 weather monitoring locations somewhat evenly distributed around the globe and at least 200 kilometers apart, we can expect that on average each year one location will have a once in 1,000 year extreme weather event (relative to that location), somewhere around the globe.  Because of random effects, some years might have none and some might have two or three stations with once in 1,000 year events.  Similarly, we can expect that on average each year two locations will have a once in 500 year event, five locations will have a once in 200 year event, ten locations will have a once in 100 year event, 20 locations will have a once in 50 year event, and 50 locations will have a once in 20 year event (for statistics relative to each location).  These statistics apply to each type of extreme weather event separately, including extreme cold temperatures, extreme hot temperatures, lengthy heat waves, lengthy cold waves, extreme precipitation amounts, lengthy wet periods, and lengthy droughts.

The point is that with news media today reporting extreme weather events around the globe, there will be many very extreme weather events reported somewhere around the globe every year.  This situation is to be expected as a part of normal weather and climate conditions and is nothing unusual.

To evaluate whether there are any significant trends over time for extreme events is difficult and requires long periods of weather data.  From a global perspective, the necessary weather data records are insufficient spatially and temporally to determine any significant trends at present.  From an individual location perspective, there are a few locations with long periods of record where it may be possible to evaluate changes over time by comparing non-overlapping 30-year periods.  Ideally at least 150 years of complete data would be needed from a single location to have five different 30-year periods to compare for trend analysis, but very few locations have enough complete weather data for that length of time.  Consequently, we cannot have much confidence in any claimed trends for extreme weather events until weather data are accumulated over much longer time spans, ideally 200 to 300 years or more, for examining trends over time.

Global Daily Temperatures Since 1948

I finally completed downloading gridded daily average global surface air temperatures based on initial condition output for the Sigma 0.995 level from the National Centers for Environmental Prediction and National Center for Atmospheric Research Reanalysis 1 (NCAR R1) cooperative effort.  This output is still being updated daily about 2 days behind the current day and extends back to 1948.  The NCAR R1 model daily temperature grids are composed of 2.5 degree latitude-longitude sectors covering the entire globe (73 by 144 grid cells).   The Sigma 0.995 level corresponds to the pressure altitude at 99.5 % of the surface air pressure, which is roughly about 50 meters above ground level. The actual height above ground level varies somewhat depending on atmospheric conditions.  I compiled daily averages for the globe [90N-90S], northern hemisphere (NH) [0-90N], southern hemisphere (SH) [0-90S], and five latitudinal zones:  Arctic [60N-90N], Northern Hemisphere mid latitudes (NH Mid) [30N-60N], Tropics [30N-30S], Southern Hemisphere mid latitudes (SH Mid) [30S-60S], and Antarctic [60S-90S].  Note that each polar zone only covers about 7% of the earth’s surface and each mid-latitude zone covers about 14%, while the Tropics, NH, and SH zones each cover about 50% of the global surface area.  The methodology and data sources are described in my previous post.

Prior to the satellite era, which began in earnest in the 1970’s, temperature data were much more sparse, especially over the oceans, but this issue also impacts all other approaches for estimating global and zonal temperatures and temperature anomalies.  I have calculated temperature  anomalies for the NCAR R1 data set as described in the previous post.  So for this post I am presenting the direct mean surface air temperature (MSAT) estimates output by the reanalysis coupled atmospheric-ocean-land modeling.  Figures 1 through 9 present the global and zonal daily MSAT averages since 1948 along with running 365-day averages to help highlight the general trends over time.  Pronounced annual seasonal temperature cycles are evident in each graph.  Click on any graph to see a larger copy.

Figure 1. NCAR R1 Global MSAT 1948-2019

Figure 2. NCAR R1 NH MSAT 1948-2019

Figure 3. NCAR R1 SH MSAT 1948-2019

Figure 4. NCAR R1 Arctic MSAT 1948-2019

Figure 5. NCAR R1 NH Mid MSAT 1948-2019

Figure 6. NCAR R1 Tropics MSAT 1948-2019

Figure 7. NCAR R1 SH Mid MSAT 1948-2019

Figure 8. NCAR R1 Antarctic MSAT 1948-2019

For a closer examination of temperatures during the current century so far (beginning 2001), I am providing Figures 9 through 14.  These graphs are in the same format as the previous graphs, but show more detail because of the much shorter time span.

Figure 9. NCAR R1 Global MSAT 2001-2019

Figure 10. NCAR R1 Tropics MSAT 2001-2019

Figure 11. NCAR R1 NH Mid MSAT 2001-2019

Figure 12. NCAR R1 SH Mid MSAT 2001-2019

Figure 13. NCAR R1 Arctic Mid MSAT 2001-2019

Figure 14. NCAR R1 Antarctic MSAT 2001-2019

In the last set of graphs below I have isolated the 365-day running mean temperatures for comparison.  Click on any graph to see a larger image.

Figure 15. NCAR R1 Global and Zonal 365-day running MSAT 1948-2019

Figure 16. NCAR R1 Global and Hemispheric 365-day running MSAT 1948-2019

Figure 17. NCAR R1 Tropics 365-day running MSAT 1948-2019

Figure 18. NCAR R1 NH Mid and SH Mid 365-day running MSAT 1948-2019

Figure 19. NCAR R1 Polar 365-day running MSAT 1948-2019

I will let the graphs speak for themselves rather than trying to offer any interpretation.

Global Temperature Reanalysis Baseline Comparisons

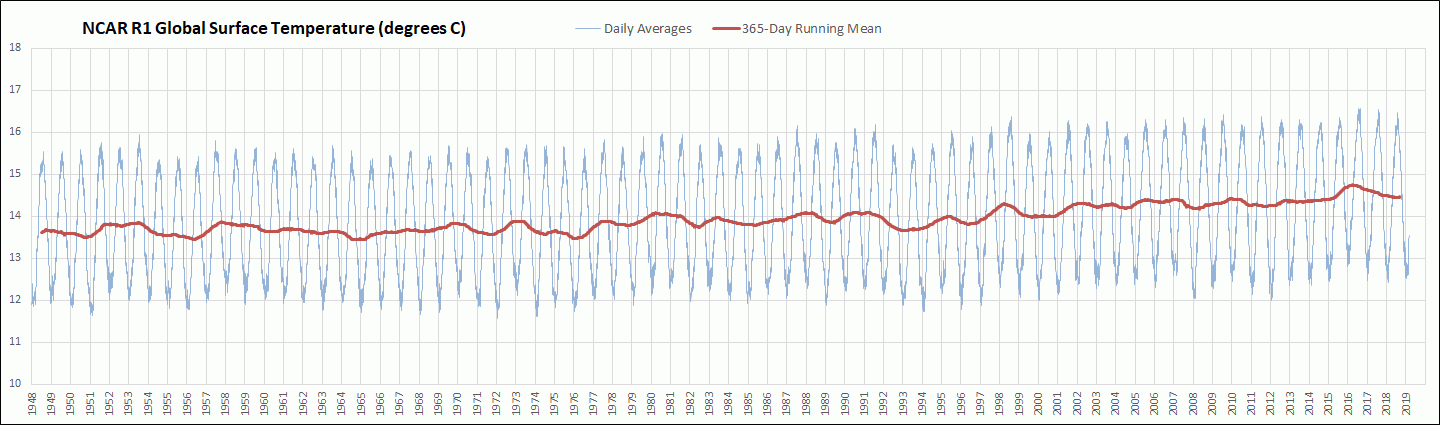
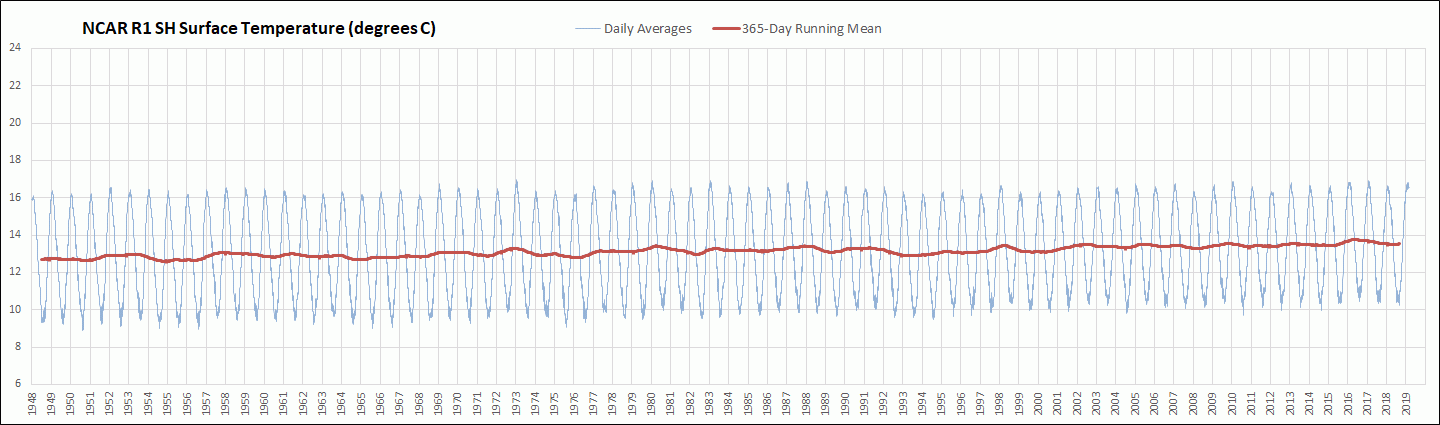
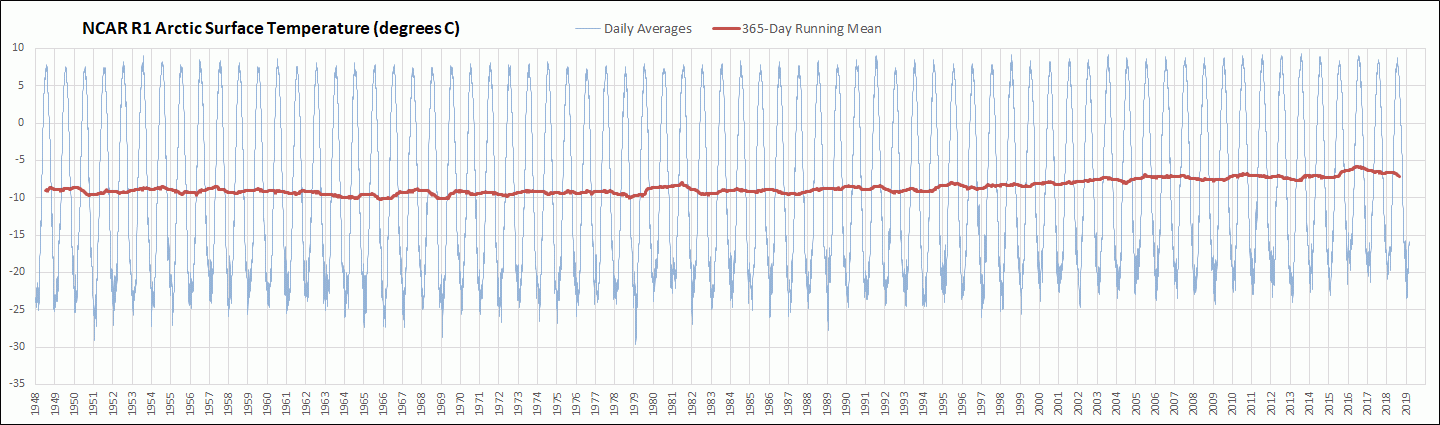
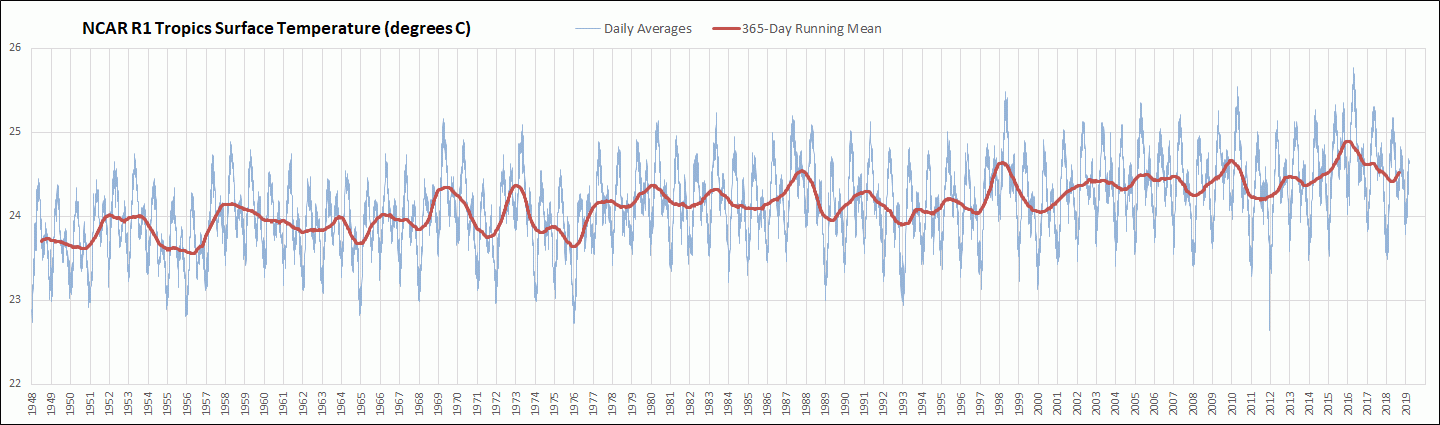
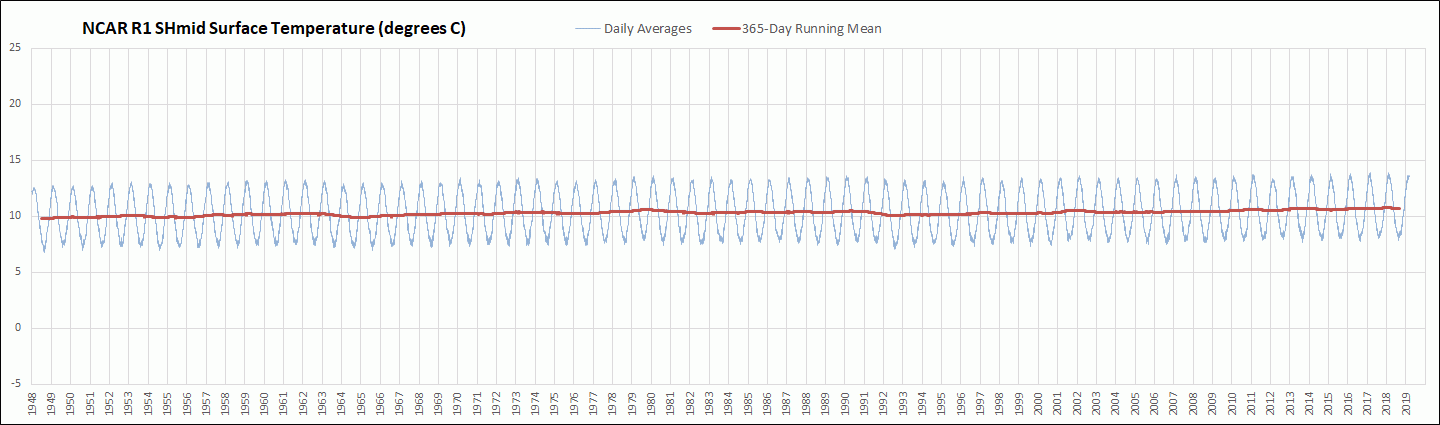
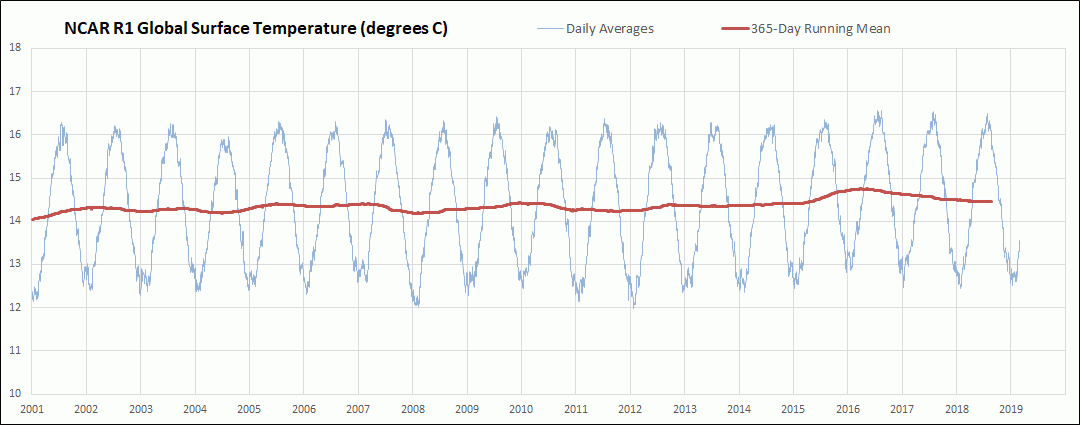
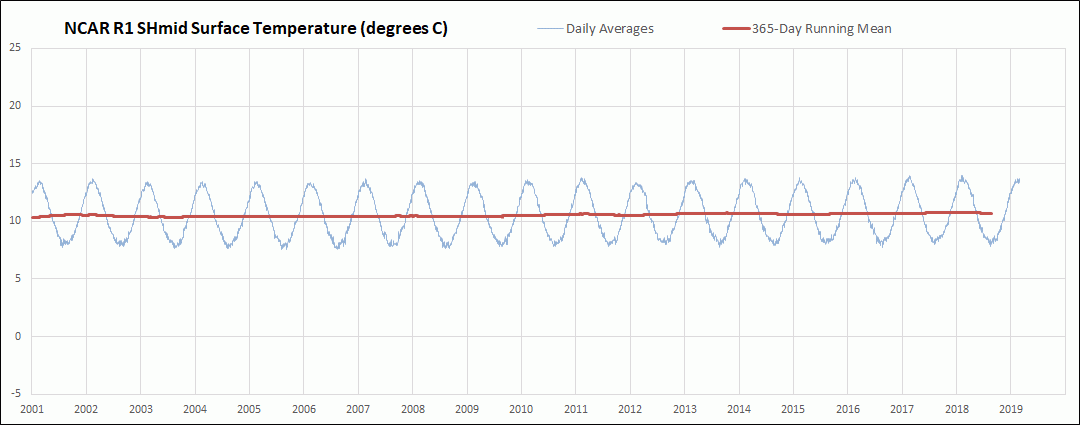
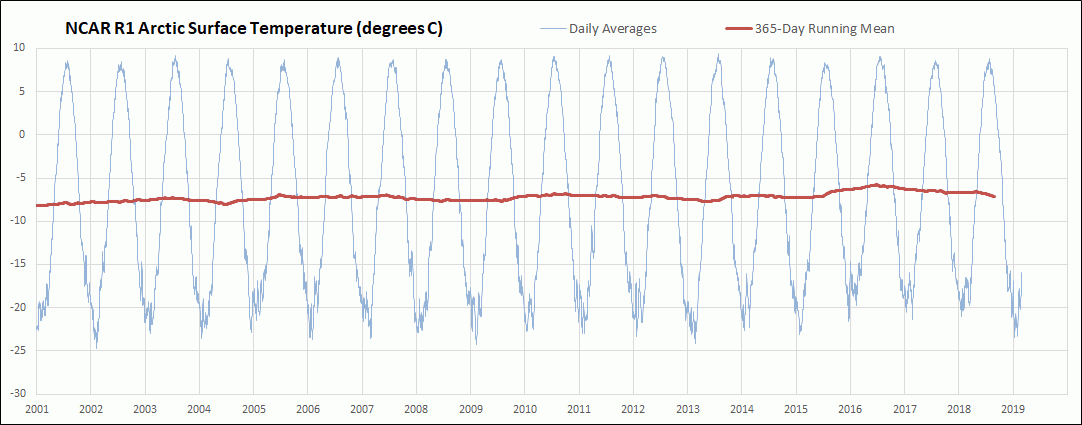
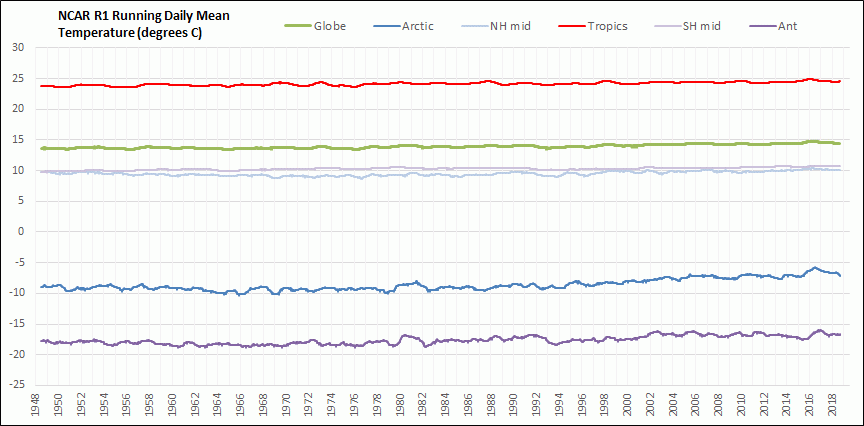
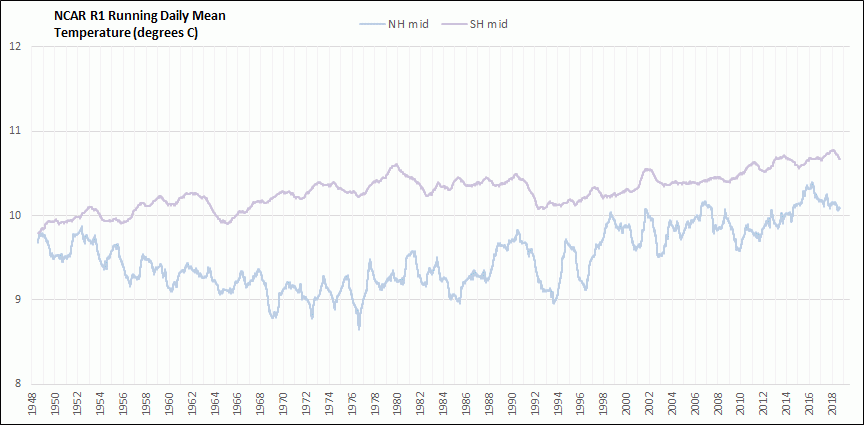
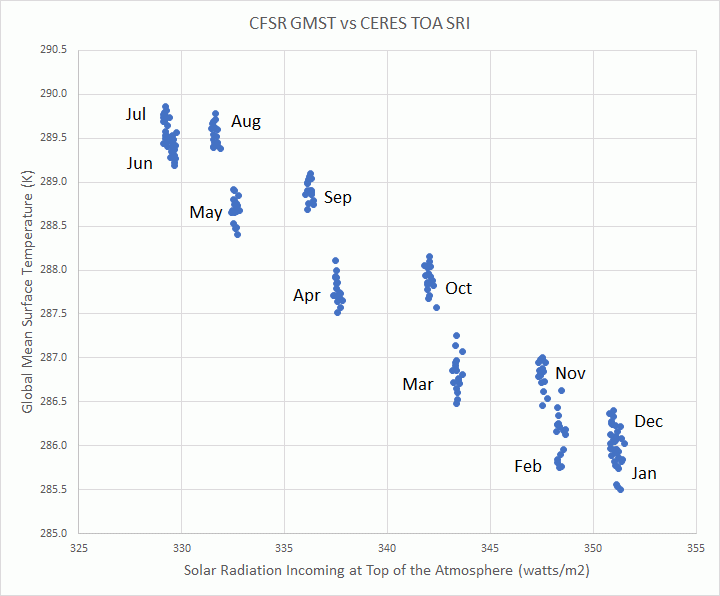
I have been downloading the daily average global surface air temperature data initial condition output for the Sigma 0.995 level from the National Centers for Environmental Prediction and National Center for Atmospheric Research Reanalysis 1 (NCAR R1) cooperative effort.  This output is still being updated daily about 2 days behind the current day and extends back to 1948.  So far I have downloaded and processed the daily temperature output back to 1979.  The Sigma 0.995 level corresponds to the pressure altitude at 99.5 % of the surface air pressure, which is roughly about 50 meters above ground level.  The actual height above ground level varies somewhat depending on atmospheric conditions.  The NCAR R1 model uses a 2.5 degree latitude by 2.5 degree longitude grid.  In this post I am comparing the resulting global mean surface air temperature anomalies (GMSATA) for several time periods and different reference baseline periods.  See the Methods section at the end for calculation details and links to sources.

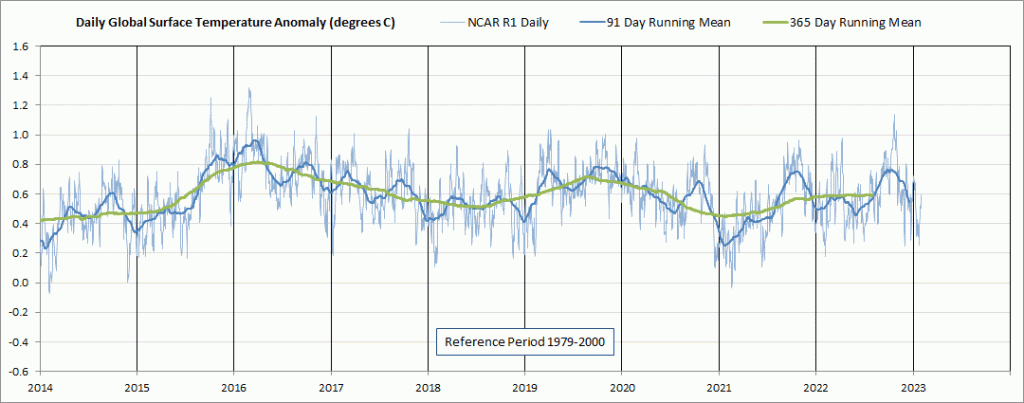
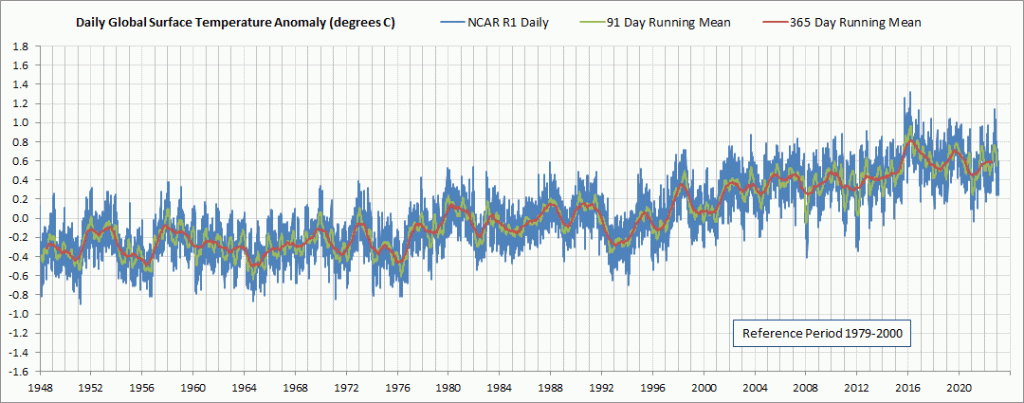
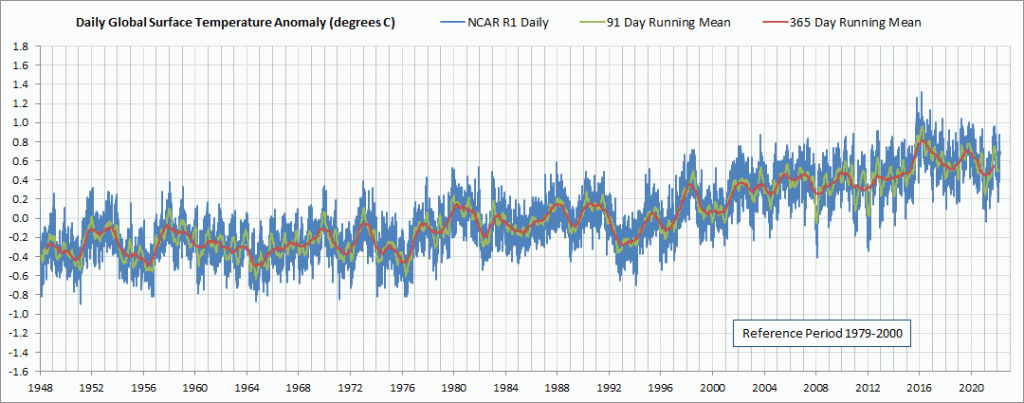
The first two graphs, Figures 1 and 2, display NCAR R1 daily average GMSATA time series output for two different reference baselines.  I was expecting the older 1979-2000 baseline to show higher temperature anomalies than the much more recent 2011-2015 baseline as can be seen in the graphs, but I was surprised that the baseline shift also changed the seasonal pattern across each year.  Apparently the seasonal patterns have shifted from one baseline period to another.  Figure 3 is provided to compare the daily average 2-meter above ground level surface air temperature anomalies from the more modern Climate Forecast System Reanalysis (CFSR)  to the NCAR R1 output.  The CFSR has a higher resolution of 0.5 degree latitude by 0.5 degree longitude.  See the Daily Updates page, which can be accessed from the menu bar at the top of this page, for more information about the daily CFSR output.  Click on any of the graphs to see a larger copy.

Figure 1. NCAR R1 GMSATA daily 2018 through 2019 February 17, referenced to 2011-2015 baseline

Figure 2. NCAR R1 GMSATA daily 2018 through 2019 February 17, referenced to 1979-2000 baseline

Figure 3. CFSR GMSATA daily 2018 through 2019 February 18, referenced to 1979-2000 baseline

I also calculated GMSATA for two other reference baseline periods, 1994-2013 and 1981-2010.  The time series results for all four reference baseline periods for 2018-2019 are plotted together in Figure 4.  They all converge around January-February and diverge the most around September-October.  I’m not sure why.

I included the 1994-2013 reference period used by Nick Stokes for reporting daily averages here and the 1979-2000 period used by the University of Maine Climate Reanalyzer here.  The 1981-2010 period is the most recent three decade (30-year) period commonly used for climatological data reporting.  I previously used the 2011-2015 period for comparing monthly NCAR R1 versus CFSR temperature anomalies here.

Figure 4. NCAR R1 GMSATA 2018 through 2019 February 17 reference baseline comparisons

The next three graphs, Figures 5 through 7, are like the first three graphs, but covering a longer time period, from 2014 to 2019 so far.  Again the general patterns are similar, but the details differ.

Figure 5. NCAR R1 GMSATA daily 2014 through 2019 February 17, referenced to 2011-2015 baseline

Figure 6. NCAR R1 GMSATA daily 2014 through 2019 February 17, referenced to 1979-2000 baseline

Figure 7. CFSR GMSATA daily 2014 through 2019 February 18, referenced to 1979-2000 baseline

The last two graphs in Figures 8 and 9 cover a longer time period, for the current century so far, beginning in 2001.  I do not yet have CFSR daily averages for all of this period, so only the NCAR R1 results for two different reference periods are presented.

Figure 8. NCAR R1 GMSATA daily 2001 through 2019 February 17, referenced to 2011-2015 baseline

Figure 9. NCAR R1 GMSATA daily 2001 through 2019 February 17, referenced to 1979-2000 baseline

Overall, this exercise goes to show that changing reference baseline periods for daily GMSATA does cause quite a bit of variation in the results – more than I expected.  However, the general trends as indicated by the running 365-day averages did not appear to be affected by changing baselines.

Methods

For the NCAR R1 daily averages I downloaded the gridded Sigma 0.995 level temperature output which is provided in compacted annual files (thanks to Nick Stokes for providing the link below on his blog).  I used the National Aeronautic and Space Administration (NASA) Panopoly program to extract the temperature grids from the compacted data files and then loaded the daily temperature grid data into spreadsheets by year.  For each day I calculated daily averages by latitude zone, weighted by area, to compile zonal and global averages.

I calculated the reference period baseline averages for each day and used centered running 5-day averages to smooth the baseline results.  Once the reference baseline temperatures were calculated, the temperature anomalies were calculated for each day by subtracting the reference baseline value for the day from the actual daily temperature average for that day.  For the temperature anomalies I also calculated running 365-day and 91-day averages to show annual and seasonal scale tendencies.

NCAR R1 annual compacted files with daily global temperature grids:
ftp://ftp.cdc.noaa.gov/Datasets/ncep.reanalysis.dailyavgs/surface/

NASA Panoply program:
https://www.giss.nasa.gov/tools/panoply/

Update 2019 February 19

I have updated all of the graphs in Figures 1-9 to the latest available date in order to match additional graphs provided below in Figures 10-13.  I am adding Figures 10-12 to present graphs of the 1994-2013 baseline results for comparison with corresponding graphs above using 2011-2015 and 1979-2000 baselines.

Figure 10. NCAR R1 GMSATA daily 2018 through 2019 February 17, referenced to 1994-2013 baseline

Figure 11. NCAR R1 GMSATA daily 2014 through 2019 February 17, referenced to 1994-2013 baseline

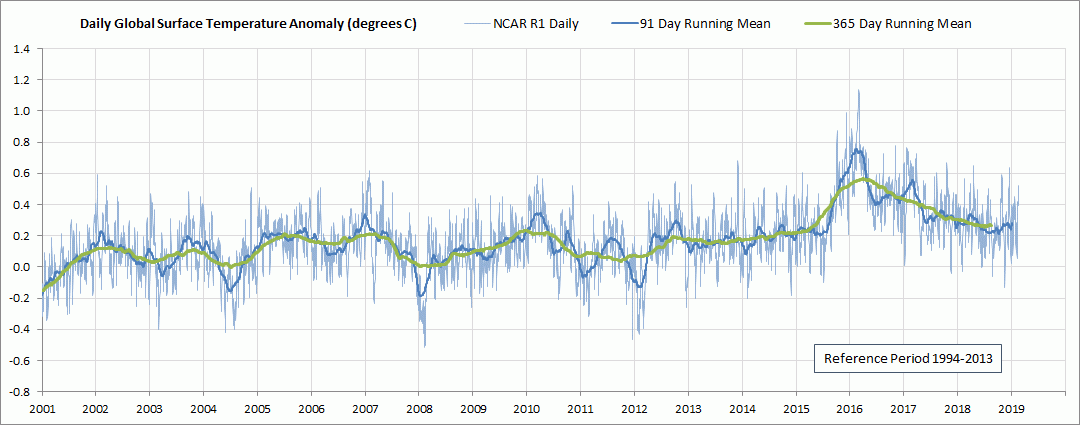
Figure 12. NCAR R1 GMSATA daily 2001 through 2019 February 17, referenced to 1994-2013 baseline

Figure 13 shows the actual baseline global mean surface air temperatures (GMSAT) for consideration regarding Figure 4.  As in that figure, the different baselines show a convergence for December through February and a divergence that peaks around August to October.  I am not sure how much is a real atmospheric change over time, or how much could be some kind of artificial change induced by variations in the input data over time.

Figure 13. NCAR R1 GMSAT reference baseline comparisons

Figure 14 shows the difference in the GMSAT from the 2011-2015 baseline minus the 1979-2000 baseline.  The largest increases since 1979-2000 were from August to October and the smallest increases were in January and February.  I am not certain if the distribution of these changes is dominated by real atmospheric changes or if there are significant artificial changes induced by changing data inputs over time that influence the seasonal distribution and magnitudes.

Figure 14. NCAR R1 GMSAT reference baseline difference 2011-2015 minus 1979-2000

As I process additional NCAR R1 output back to 1948, I plan to evaluate and compare some additional reference baselines, including overlapping 3-decade baselines beginning with 1951-1980.  I also plan to look at the baseline variations in the hemispheric as well as 30 degree latitude zones and the results will be presented in future posts.

Update 2019 March 1

I finished loading and processing all of the NCAR R1 daily GMSAT data back to 1948 and I am adding below some additional baseline comparisons.  Figure 15 compares the effects of using different baselines to evaluate the last year of daily GMSATA, similar to Figure 4 above.  Here the baselines compared are overlapping 3-decade periods from 1981-2010 back to 1951-1980.

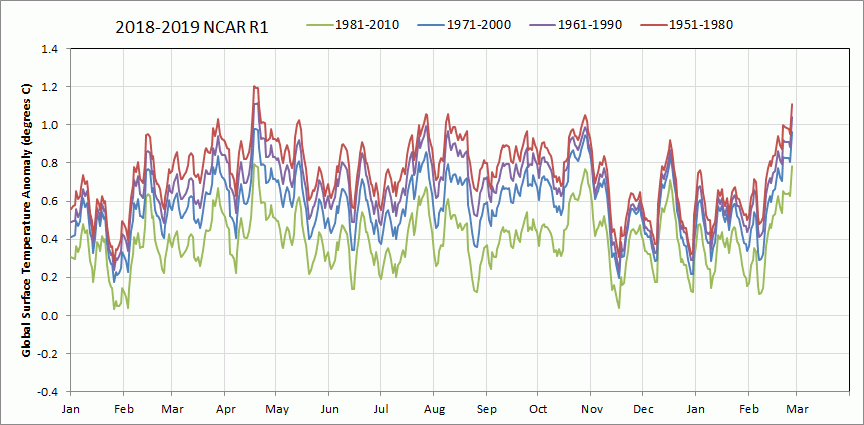
Figure 15. NCAR R1 GMSATA 2018 through 2019 February 28 reference baseline comparisons back to 1951-1980

Figure 16 compares the actual baseline daily GMSAT averages for all of the baselines I have analyzed so far, including those previously provided in Figure 13 above.

Figure 16. NCAR R1 GMSAT reference baseline comparisons back to 1951-1980

Figures 17 and 18 show the daily GMSAT changes from subtracting different baselines for the periods indicated in each graph.

Figure 17. NCAR R1 GMSAT reference baseline difference 2011-2015 minus 1951-1980

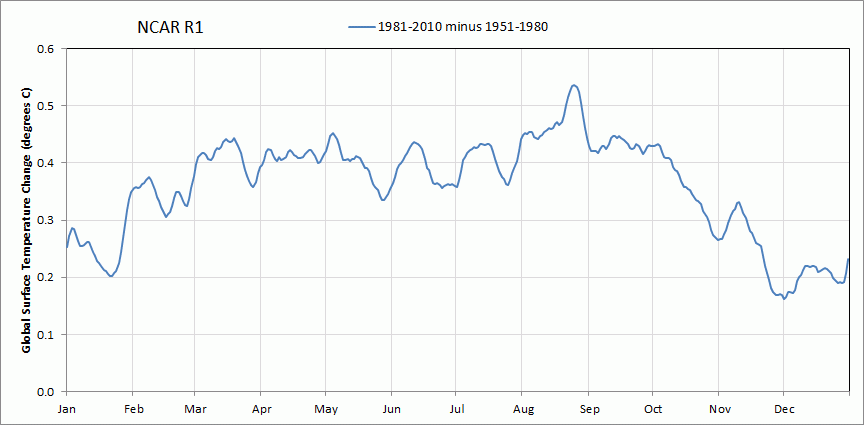
Figure 18. NCAR R1 GMSAT reference baseline difference 1981-2010 minus 1951-1980

In conclusion, it is apparent that changing baselines does effect the seasonal patterns in the daily GMSATA results, but does not effect the general annual patterns as indicated by the running 365-day averages.

Update 2019 March 2

I’m adding two animated GIF graphs to better illustrate my conclusion above. The animations in Figures 19 and 20 compare NCAR R1 daily GMSATA referenced to 2011-2015 in comparison to 1994-2013 and 1951-1980 baselines respectively.  Notice that the running 365-day average pattern does not change as the baseline changes, but the seasonal patterns change significantly.  I suspect that some of the seasonal changes are real and at least part of the changes are artificial because of changing data inputs over time (especially for periods prior to satellite observations, such as the 1951-1980 baseline).  Click on either figure to see a larger copy.

Figure 19. Animation comparing the NCAR R1 GMSATA for 2001-2019 using two different reference baseline periods, 2011-2015 versus 1994-2013

Figure 20. Animation comparing the NCAR R1 GMSATA for 2001-2019 using two different reference baseline periods, 2011-2015 versus 1951-1980

Update 2019 May 5

Here are two more graphs comparing GMSAT changes from one baseline to another.  Notice that the largest increases in GMSAT have been in the August to October range, with the lowest increases in December and January.  Click on either figure to see a larger copy.

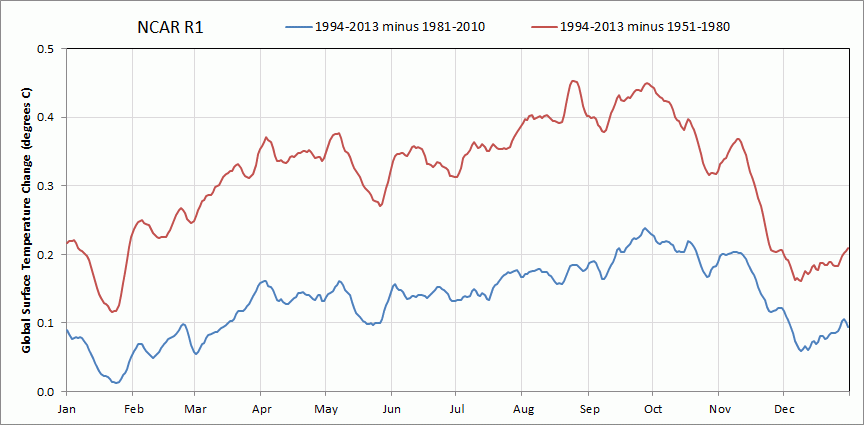
Figure 21. NCAR R1 GMSAT reference baseline difference 1994-2013 minus 1981-2010 and 1994-2013 minus 1951-1980

Figure 22. NCAR R1 GMSAT reference baseline difference 1981-2010 minus 1951-1980

GOES-17 Is Now Operational

“In its new role, GOES-17 will serve as NOAA’s primary geostationary satellite for detecting and monitoring Pacific storm systems, fog, wildfires, and other weather phenomena that affect the western United States, Alaska, and Hawaii.”

“The latest milestone for GOES-17 comes exactly eleven months after the satellite first reached its geostationary orbit 22,000 above Earth. Launched March 1, 2018, GOES-17 is NOAA’s second advanced geostationary weather satellite and the sister satellite to GOES-16 (also known as GOES East). Together the two satellites provide high-resolution visible and infrared imagery as well as lightning observations of more than half the globe – from the west coast of Africa to New Zealand, and from near the Arctic Circle to the Antarctic Circle.”

Large winter storm system moving into California 2019 February 2:

High resolution animation of clouds around Hawaii 2019 January 15:

High resolution animation of brown smoke plume blowing toward the west from the large from the Woolsey Fire west of Los Angeles  in California, as high level cirrus clouds above blow to the east on 2018 November 13:

Read more here.

Real-time images here.

The climate is changing!

The climate is changing!
The climate is changing!
The climate is changing!

And its all YOUR FAULT!!!

Say the Chicken Littles of today.

Mostly for pride, prestige, fame, and funding.
And to promote potentially catastrophic policies.
All in the false pretense of “green” and “renewable” energy.
Endeavors that will enrich the Chicken Littles promoting them.
Ironically these policies are not likely to stop climate change.
But will instead impoverish and endanger most of us.
Wasting huge amounts of hard earned tax payer dollars.

And to top it all off …
The hidden Chicken Little motto:
Do as I say, not as I do.
Hypocrisy at its best.

Chicken Littles of the world are in a class of their own.
Not subject to the rules they espouse for the rest of us.
They say we must quit using fossil fuels.
But that is not what they do:
Flying in private jets. Living in huge walled mansions.
Driving expensive cars. Living lavish lifestyles.
All provided by fossil fuels.

Climate change is now blamed for almost everything bad.
Never mind digging for real causes that are ignored.

Consequently, “climate change” has become a religion.
We must have faith in the sacred climate models.
Never mind that they have not been validated.
The unfaithful are persecuted as “deniers”.

When will the gullible public learn?
When lies are told often enough.
They are perceived as truth.
Buyer beware.

How the climate models fare

The graph below provided by Clive Best compares global surface air temperature anomaly projections from a large number of climate model runs for different Representative Concentration Pathways (RCPs) for carbon dioxide versus two estimates of global surface air temperature anomalies based on actual temperature measurements from Cowtan and Way and the UK Hadley Climate Research Unit Temperatures (HadCRUT4.6).  Notice that the measurement based estimates are indicating global temperatures at the low end of the model projections.

Not at all alarming.

Actual climate model temperature projections

Another graph from Clive Best below shows direct climate model output of projected global average surface air temperatures, indicating a very wide range in temperatures that is hidden by using temperature anomalies in the graph above.  Another sign that the climate models are not representing the real world very well.

Graphs sourced here, thanks to Clive Best.

And if you think climate is changing now, take a look at how much climate has changed in the last 3 million years without any help from humans:
Paleo Climate

Earth Orbital Eccentricity Effect on Global Mean Surface Temperature

I thought it would be an interesting exercise to look at the annual change in global mean surface temperature (GMST) in the atmosphere at 2 meters above ground level versus the annual change in solar radiation incoming (SRI) at the top of the atmosphere (TOA).

The earth’s orbit is slightly elliptical.  Eccentricity is a measure of the departure of an ellipse from a true circle.  The earth’s eccentricity varies over long time scales and is estimated to have ranged from a low of 0.000055 to a high of 0.0679, with a geometric mean of 0.0019.  The present eccentricity is 0.017 and decreasing very slowly.  That doesn’t seem like much, but the earth’s distance from the sun currently increases by 3.4% over the course of a year from the minimum distance in early January to the maximum distance in early July.  That variation in distance causes about a 6.8% increase in TOA SRI relative to the minimum amount at the greatest distance in early July in order to reach the maximum amount at closest distance in early January, assuming a constant output of radiation from the sun.

The US National Aeronautical and Space Administration (NASA) Clouds and the Earth’s Radiant Energy System (CERES) measurements from satellites include TOA SRI.  I downloaded monthly CERES TOA SRI for the period from March 2000 through July 2018.  I also have compiled monthly estimates of GMST from the Climate Forecast System Reanalysis (CFSR) output of initial conditions four times per day, with monthly data prior to 2010 provided by the University of Maine Climate Change Institute (UM CCI) and data from 2010 through 2018 calculated from the Climate Data Assimilation System (CDAS) output of 2-meter surface air temperature.

A time series graph comparing TOA SRI with GMST is provided in Figure 1 below (click to enlarge).  It shows the annual cycle of GMST with a peak in July and minimum in January, whereas the TOA SRI peaks in July with a minimum in January – the complete opposite.  At first, this seems counter-intuitive since increased incoming solar radiation should cause increased temperature and yet the data show the opposite.  My guess is that there is a time lag mediated primarily by the oceans and possibly also affected by the much greater percentage of land in the northern hemisphere, but I have not read up on the subject.  This graph also includes centered running 12-month averages (Run 12) for both TOA SRI and GMST.

Figure 1. Comparison of CERES TOA SRI with CFSR GMST
(click to enlarge)

Figure 2 below compares the CERES TOA SRI with the CFSR Northern Hemisphere (NH) mean surface temperature.  The phase of the annual cycle in temperature is similar to that of the global temperature cycle and is nearly opposite the phase of the TOA SRI cycle.  Notice that the amplitude of the annual temperature cycle is much larger than the global cycle.

Figure 2. Comparison of CERES TOA SRI with CFSR Northern Hemisphere Mean Surface Temperature (click to enlarge)

Figure 3 below compares the CERES TOA SRI with the CFSR Southern Hemisphere (SH) mean surface temperature.  The phase of the annual cycle in temperature is very close to the phase of the TOA SRI cycle, but advanced forward by about a month.  Notice that the annual temperature cycle is larger than the global cycle, but not near as large as the NH cycle.

Figure 3. Comparison of CERES TOA SRI with CFSR Southern Hemisphere Mean Surface Temperature (click to enlarge)

Figure 4 below compares the CERES TOA SRI with the CFSR tropics (30N-30S) mean surface temperature, which covers the 50% of the global surface that receives most of the incoming solar energy.

Figure 4. Comparison of CERES TOA SRI with CFSR Tropics Mean Surface Temperature (click to enlarge)

The not quite linear cyclical nature of the relationship between SRI and GMST is illustrated by the scatter plot in Figure 5 below.

Figure 5. Scatter plot of CFSR GMST versus CERES TOA SRI
(click to enlarge)

By lagging the GMST by 6 months, the relationship to TOA SRI looks more meaningful, as seen in Figure 6 below.

Figure 6. Scatter plot of CFSR GMST lagged 6 months versus CERES TOA SRI
(click to enlarge)

I calculated and compiled annual statistics for each year.  During the study period, the 2001-2017 TOA SRI average of the 17 annual averages was 340.023 watts per meter squared (watts/m²) with a standard deviation of only 0.087 watts/m².  The monthly averages ranged from 329.113 to 351.516 watts/m².  The annual range in monthly TOA SRI averaged 21.998 watts/m² with a standard deviation of only 0.106 watts/m².  The highest annual range was 21.838 and lowest 22.261 watts/m².  The average percentage of the annual range relative to the lowest month each year was 6.682%.  Note that I did not bother to weight the annual averages based on number of days per month because I do not expect a significant difference.

Similarly, the 2001-2017 average of the 17 annual averages of GMST was 287.810 Kelvin (K) with a standard deviation of 0.133 K and a range in monthly averages from 285.505 K to 289.864 K.  The lowest annual average was 287.735 K in 2008 and the highest was 288.051 K in 2016.  The annual range in monthly GMST averaged 3.775 K with a standard deviation of 0.166 K and varied from 3.511 K to 4.128 K.

For 2001-2017, the CFSR monthly surface temperature data shows an average annual range of 12.589 K for the northern hemisphere and an average annual range of 5.227 K for the southern hemisphere. The southern hemisphere cycle is only one month delayed from the TOA SRI cycle. Both of the hemispheric cyclical temperature swings are larger than the global swing and include both seasonal earth tilt plus eccentricity effects. The global swing should be the net remainder resulting from the eccentricity induced TOA SRI effect.

Initial Thoughts

So, if we assume that the annual range in TOA SRI is the primary driver for the annual range in GMST, then we can calculate that GMST rises (or falls) by 3.775/21.998 = 0.172 K per 1 watt/m² of TOA SRI change.  The implication is that if a doubling of CO₂ causes a radiative forcing of 3.7 watts/m², the corresponding rise in GMST would be 3.7 x 0.172 = 0.635 K and this would include any feedbacks that normally occur in the earth system over an annual cycle.  The main difference is that the ramp up in solar input from orbital eccentricity occurs over only a 6 month period each year, whereas the doubling of CO₂ might take on the order of a century.  However, both are responses to changes to the earth’s radiation balance.  So far, I have not been able to think of any compelling reasons why the difference in time scales would make much difference in the resulting effect on GMST.  Possibly the short period cycling of the solar input may not allow enough time to reach full impact on GMST in either direction, leading to a quasi-steady state oscillating result?

I’m afraid this assessment may be too simplistic or that I may have overlooked some important influences.  Thus, I’m not at all certain this approach is a valid method for estimating the effect on GMST from a doubling of CO₂.  I will be interested hear what readers have to say and I would be especially interested in learning how well the global climate models handle this annual cycling of both TOA SRI and GMST.

After Further Review

I’m now seeing that the annual cycle in global temperature is dominated by the seasonal cycle related to the earth’s axial tilt.  I thought it might still be possible to estimate the effects of eccentricity on the seasonal cycle in each hemisphere, and from that result, estimate the net effect on the global temperature cycle from eccentricity.  However, I found that backing out a rough estimate of the effect of eccentricity actually increased the global annual temperature range, because it increases the NH annual temperature range more than it decreases the SH annual temperature range.  Consequently it does not appear possible to determine the effect of eccentricity on global temperature without using a climate model to test the effect of varying degrees of eccentricity.  Like many things I’m learning about climate … it is very complex.

References

Eccentricity discussion:
https://en.wikipedia.org/wiki/Milankovitch_cycles

CERES project description:
https://en.wikipedia.org/wiki/Clouds_and_the_Earth’s_Radiant_Energy_System

CERES data download:
https://ceres.larc.nasa.gov/order_data.php

UM CCI Reanalyzer:
https://climatereanalyzer.org/

CDAS monthly average downloads:
https://nomads.ncdc.noaa.gov/modeldata/cfsv2_analysis_monthlymeans_pgb/

Climate sensitivity discussion:
https://en.wikipedia.org/wiki/Climate_sensitivity

Earth’s energy budget discussion:
https://en.wikipedia.org/wiki/Earth%27s_radiation_balance